
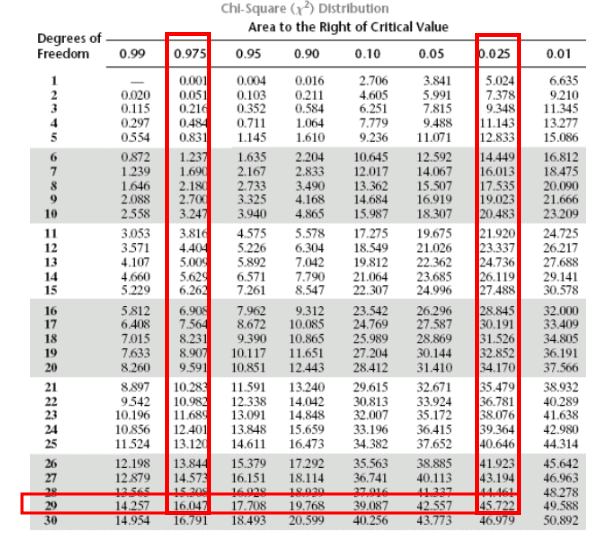
Typically we would simply use R to look this up qchisq(c(0.05), df=1, lower.tail=FALSE)īut we can also get this from the table of critical values (Fig. What is the critical value of the chi-square distribution at 5% and one degree of freedom?. For now, we report the Chi-square test statistic for this test was 3.1264 and the test had one degree of freedom. Was there a survival difference between male and female House Sparrows? This is a classic contingency table analysis, something we will at length in Chapter 9. Survival statistics of Bumpus House sparrows We’ll look at this data set when we introduce Linear Regression. Bumpus made several measures of morphology on the birds and the data set has served as a classical example of Natural Selection ( Chicago Field Museum).
The birds were collected from the ground 72 of the birds survived, 64 did not (Table 1).

Professor Hermon Bumpus of Brown University in Providence, Rhode Island, received 136 House Sparrows ( Passer domesticus) after a severe winter storm 1 February 1898. See Appendix for a complete chi-square table. Portion of the table of some critical values of chi-square distribution, one tailed (right-tailed or “upper” portion of distribution). A portion of the critical values of the chi-square distribution are shown in Figure 3.įigure 3. The justification for this approach to testing of statistical significance is developed in Chapter 8. You are not expected to be able to follow this logic just yet - rather, we teach it now as a sort of mechanical understanding to develop in the NHST tradition. If our test statistics is greater than the critical value, then the p-value of our results are less than 5% (R will report an exact p-value for the test statistic). The interpretation of the result is as follows: after calculating a test statistic, we can judge significance of the results relative to the null hypothesis expectation. The critical value is defined as the value of the test statistic - the cutoff boundary between statistical significance and insignificance - that occurs at the Type I error rate, which is typically set to 5%. In this case, probability of values greater than the critical value.īy convention in the Null Hypothesis Significance Testing protocol (NHST), we compare the test statistic to a critical value. The test of the chi-square is typically one-tailed. Thus tests using the chi-square are one-tailed (Fig.
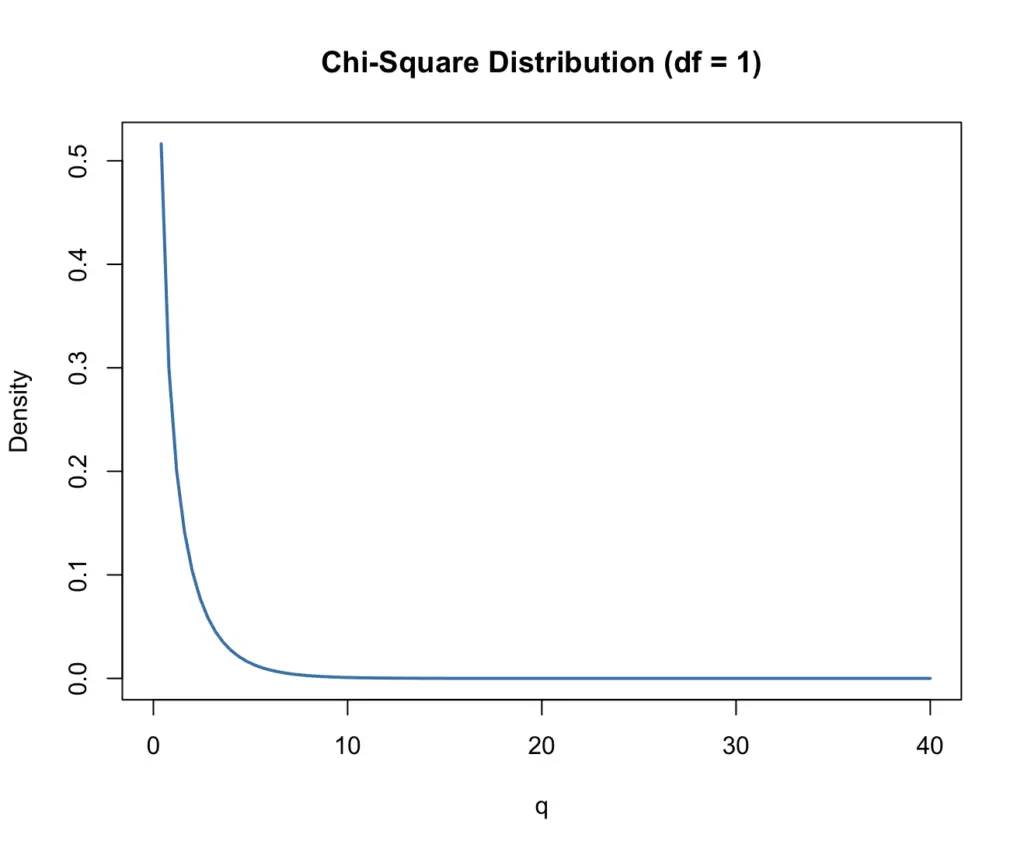
Note that the distribution is asymmetric, particularly at low degrees of freedom. Animated GIF of plots of chi-square distribution over range of degrees of freedom. We evaluate how often that value or greater of a test statistic will occur by applying the chi-square distribution function. Graphs to show chi-square distribution for degrees of freedom equal to 1 – 5, 10, and 20 (Fig. We call the result of this calculation the chi-square test statistic. Where k is the number of groups or categories, from 1 to k, and f i is the observed frequency and f i “hat” is the expected frequency for the k th category. 8.) We will use the chi-square distribution to test statistical significance of categorical variables in goodness of fit tests and contingency table problems. (The number of independent pieces of information needed to calculate the estimate, see Ch. The chi-square distribution describes the probability distribution of the squared standardized normal deviates with degrees of freedom, df, equal to the number of samples taken. As noted earlier, the normal deviate or Z score can be viewed as randomly sampled from the standard normal distribution. What is chi square and what is a chi squared distribution?Ī chi squared distribution comes from the chi square statistic, which measures how different are observed values from the expected ones from a true hypothesis in a statistical test. In todays lesson we will learn what is chi square in statistics and how do we use it when constructing confidence intervals. With a 99% confidence level what is the range of standard deviation that this machine will output per bottle? After making 41 bottles they find that their bottles have an average of 335mL of liquid with a standard deviation of 3mL. Determining the Confidence Interval for Standard DeviationĪ Soda-pop company "Jim's Old Fashion Soda" is designing their bottling machine.With a 90% confidence level give a range where the variance of all road and racing bicycle wheels lie. From a sample of 15 bicycles it was found that the wheel diameters have a variance of 10mm. Road and racing bicycles have an average wheel diameter of 622mm. Determining the Confidence Interval for Variance.If a Chi-Squared distribution has 8 degrees of freedom find X R 2 X_R^2 X R 2 and X L 2 X_L^2 X L 2 , with a Determining the Critical Value for a Chi-Square Distribution ( X R 2 (X_R^2 ( X R 2 and X L 2 ) X_L^2) X L 2 ).How many degrees of freedom does a sample of size,


 0 kommentar(er)
0 kommentar(er)
